충돌의 물리학
우리는 지금까지 벡터, 힘과 운동, 만유인력, 입자계 등 여러 물리학 개념들을 프로그램으로 구현해 보았습니다. 그러나 잘 생각해 보면 정말 중요한 충돌에 대해서는 거의 살펴본 적이 없었네요.
물론 전혀 없었던 것은 아니었습니다. 공이 바닥에 충돌하여 튀어오르는 상황을 구현해 본적이 있는데 기억나시죠? 앞으로 다뤄볼 충돌은 바닥과의 충돌보다 복잡한 입자들 사이의 충돌을 다뤄보려고 합니다. 그러기 위해서는 다음과 같은 두가지 알고리즘을 구현해야 합니다.
- 두 물체가 충돌했다는 것을 어떻게 확인할 것인가?
- 두 물체의 충돌 후 속도는 어떻게 구할 것인가?
1. 충돌 감지
첫 번째 충돌 감지는 어떻게 알 수 있을까요? 일단 제일 간단한 두 공이 2차원으로 충돌하는 상황을 살펴보겠습니다. 충돌을 감지하기 위해서는 두 공 사이의 거리를 구해야 하는데 이는 공의 중심좌표의 차이를 통해 피타고라스 공식으로 구할 수 있습니다.
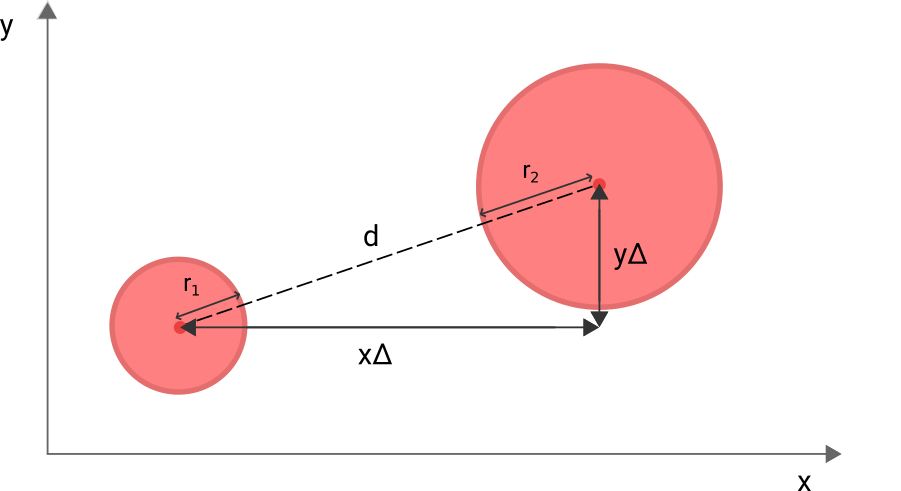
하지만 우리는 p5.js 에서 제공하는 벡터 기능을 활용하면 더 쉽게 공의 중심 사이 거리를 구할 수 있습니다. 이러한 방법은 이미 만유인력을 구할 때 사용했던 방법입니다.
- 두 공의 중심 위치를 벡터로 나타내고 Vector.sub()함수를 이용하여 두 벡터의 차를 구하여 두 공의 중심을 잇는 벡터를 구합니다.
- p5.js의 벡터 기능 중에 mag()함수를 이용하여 벡터의 크기를 구하면 두 점 사이의 거리가 나오게 됩니다.
- 두 공 중심사이의 거리가 두 공의 반지를 합보다 작으면 충돌했다고 볼 수 있습니다.
간략하게 의사 코드로 나타내면 다음과 같습니다.
충돌 감지 함수() {
공1의 반지름 = 30;
공2의 반지름 = 50;
공1 중심위치벡터 = createVector(100,100);
공2 중심위치벡터 = createVector(150,170);
두 공 중심을 잇는 벡터 = p5.Vector.sub(공2 중심위치벡터, 공1 중심위치벡터);
두 공 중심 사이 거리 = 두 공 중심을 잇는 벡터.mag();
두 공 반지름 합 = 공1의 반지름 + 공2의 반지름;
if (두 공 중심 사이 거리 <= 두 공 반지름 합) {
충돌!!!
}
}
그럼 지난 4차시의 만유인력 활동 코드를 약간 수정하여 Ball 클래스를 만들고 여러 ball 객체를 만들어 공이 충돌 조건을 만족하였을 때 공의 색이 변하게 구현해 보도록 하겠습니다.
이 때 공이 여러개 있을 때 각 공끼리 충돌하는 조건을 살펴봐야 하기 때문에 반복문을 사용합니다. 그러나 앞의 만유인력을 계산할때와는 다르게 한번 체크한 공끼리는 다시 체크할 필요가 없기 때문에 만약 공이 5개 있다면 아래와 같이 반복하면 됩니다.
balls[0].collisionDetection(balls[1]);
balls[0].collisionDetection(balls[2]);
balls[0].collisionDetection(balls[3]);
balls[0].collisionDetection(balls[4]);
balls[1].collisionDetection(balls[2]);
balls[1].collisionDetection(balls[3]);
balls[1].collisionDetection(balls[4]);
balls[2].collisionDetection(balls[3]);
balls[2].collisionDetection(balls[4]);
balls[3].collisionDetection(balls[4]);
이를 반복문으로 표현하면 다음과 같습니다.
for (let i = 0; i < 공의 갯수; i++) {
// 만유인력에서 모든 조합의 경우를 생각하는 것과 다르게
// 앞서 선택한 조합은 빼기 위해서 j = i + 1 부터 시작
for (let j = i + 1; j < 공의 갯수; j++) {
// 공과 공 사이의 충돌 여부를 체크
balls[i].collisionDetection(balls[j]);
}
}
자 그럼 활동 1을 직접 실행해보고 코드를 살펴봅시다.
활동 1. 공의 충돌 감지하기
공이 충돌 조건이 잘 구현되었나요? 공의 갯수나 색등을 변화시키면서 코드를 다시 실행해 보세요.
2. 충돌 후의 속도 구하기
앞에서 충돌 조건에 대해서 알아보았으니 다음 과정으로 충돌 후에 속도를 어떻게 구현할 수 있을 지 살펴보도록 하겠습니다. 여러분 충돌하면 생각하는 물리학 개념이 무엇이 있나요?
예 맞습니다. 바로 운동량 보존입니다. 물론 F = ma 로 충돌을 구현할 수도 있지만 운동량과 운동에너지를 활용하면 충돌을 물리학적으로 좀 더 쉽게 구현할 수 있습니다.
자 그럼 우리가 물리학 시간에 배운 두 물체가 충돌할 때의 운동량 보존법칙과 운동에너지 보존을 다시 살펴봅시다.
운동량 보존 법칙 : $m_1v_1 + m_2v_2 = m_1V_1 + m_2V_2$
충돌시 운동에너지 보존 : $\frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 \geqq \frac{1}{2}m_1V_1^2 + \frac{1}{2}m_2V_2^2$
운동에너지는 완전탄성 충돌일 경우에만 보존되며, 완전 탄성 충돌이 아닌 경우 에너지가 소리나 열로 전환되어 충돌 후의 운동에너지의 합이 충돌 전 운동에너지의 합보다 작게 됩니다.
운동량 보존 법칙과 운동에너지 보존 법칙을 하나의 공식으로 합칠 수 있는 데 ‘반발계수’라고 합니다. 반발계수식을 유도하는 과정은 다음과 같습니다.
$m_1v_1 + m_2v_2 = m_1V_1 + m_2V_2$
$m_1v_1 - m_1V_1 = m_2V_2 - m_2v_2$
$m_1(v_1 - V_1) = m_2(V_2 - v_2)$ …..(1)
$\frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 \geqq \frac{1}{2}m_1V_1^2 + \frac{1}{2}m_2V_2^2$
$\frac{1}{2}m_1v_1^2 - \frac{1}{2}m_1V_1^2 \geqq \frac{1}{2}m_2V_2^2 - \frac{1}{2}m_2v_2^2$
$\frac{1}{2}m_1(v_1^2 - V_1^2) \geqq \frac{1}{2}m_2(V_2^2 - v_2^2)$
$\frac{1}{2}m_1(v_1 + V_1)(v_1 - V_1) \geqq \frac{1}{2}m_2(V_2 + v_2)(V_2 - v_2)$
$m_1(v_1 + V_1)(v_1 - V_1) \geqq m_2(V_2 + v_2)(V_2 - v_2)$ …..(2)
(2)식을 (1)식으로 나누면
$(v_1 + V_1) \geqq (V_2 + v_2)$
$(v_1 - v_2) \geqq (V_2 - V_1)$
$1 \geqq \frac{V_2 - V_1}{v_1 - v_2} $
반발 계수 $e = 1 \geqq \frac{충돌\ 후\ 멀어지는\ 속도}{충돌\ 전\ 가까워지는\ 속도} $
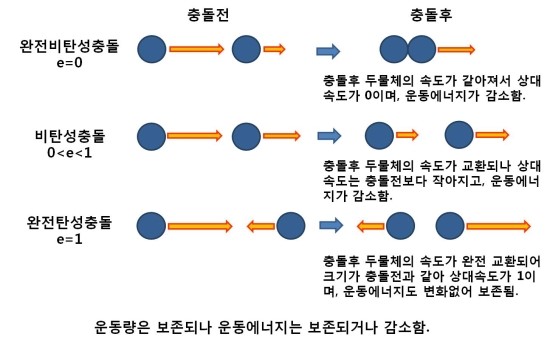
$e = 0$ : 완전 비탄성 충돌 (충돌 후 물체가 붙어서 운동)
$0 < e < 1$ : 비탄성 충돌 (운동량만 보존, 운동에너지 손실)
$e = 1$ : 완전 탄성 충돌 (운동량과 운동에너지 보존)
이 반발계수 충돌시에 질량에 의한 효과까지 적용하기 위해서 운동량 보존 공식에 다시 대입하여 충돌 후의 물체의 속도($V_1$, $V_2$)로 정리하면 다음과 같습니다.
$m_1v_1 + m_2v_2 = m_1V_1 + m_2V_2$ ….. (1) 운동량 보존
$e = \frac{V_2 - V_1}{v_1 - v_2}$
$e(v_1-v_2) + V_1 = V_2$ ….. (2) 반발계수
물체1의 충돌 후 속도 $V_1$으로 정리하기 위해서 (1)식 $V_2$에 반발계수 (2)식을 대입하면 물체2의 충돌후 속도 $V_2$식이 사라진 $V_1$이 나오게 된다.
$m_1v_1 + m_2v_2 = m_1V_1 + m_2(e(v_1-v_2) + V_1)$
$m_1v_1 + m_2v_2 = m_1V_1 + em_2v_1-em_2v_2 + m_2V_1$
$V_1(m_1 + m_2) = m_1v_1 + m_2v_2 -em_2v_1 + em_2v_2$
$V_1(m_1 + m_2) = (e + 1)m_2v_2 + v_1(m_1-em_2)$
$V_1 = \frac{(e+1)m_2v_2 + v_1(m_1-em_2)}{(m_1 + m_2)}$ …..(3) 물체1의 충돌후 속도
마찬가지로 $V_2$를 구하면 다음과 같다.
$V_2 = \frac{(e+1)m_1v_1 + v_2(m_2-em_1)}{(m_1 + m_2)}$ …..(4) 물체2의 충돌후 속도
위에서 유도한 (3),(4) 식을 통해 운동량 보존과 운동에너지 보존이 적용된 충돌 후 물체의 속도를 구할 수 있습니다. 다음 충돌 속도 공식은 1차원적으로만 적용되는 것이기 때문에 각 x, y 방향 성분 별로 적용할 수 있습니다. 그래서 아래 공식을 코드로 적용할 때는 x,y 방향으로 나누어 적용해야 합니다.
$V_1 = \frac{(e+1)m_2v_2 + v_1(m_1-em_2)}{(m_1 + m_2)}$
$V_2 = \frac{(e+1)m_1v_1 + v_2(m_2-em_1)}{(m_1 + m_2)}$
let m1 = this.m; // 물체 1의 질량
let m2 = other.m; // 물체 2의 질량
let u1 = this.vel; // 물체 1의 충돌 전 속도
let u2 = other.vel // 물체 2의 충돌 전 속도
// 충돌 후 속도 공식 사용
let v1_x = ((e + 1) * m2 * u2.x + u1.x * (m1 - e * m2))/(m1 + m2); //물체 1의 충돌후 x방향 속도
let v1_y = ((e + 1) * m2 * u2.y + u1.y * (m1 - e * m2))/(m1 + m2); //물체 1의 충돌후 y방향 속도
let v2_x = ((e + 1) * m1 * u1.x + u2.x * (m2 - e * m1))/(m1 + m2); //물체 2의 충돌후 x방향 속도
let v2_y = ((e + 1) * m1 * u1.y + u2.y * (m2 - e * m1))/(m1 + m2); //물체 2의 충돌후 y방향 속도
// 물체 1,2에 새로운 속도 적용
this.vel = createVector(v1_x,v1_y);
other.vel = createVector(v2_x,v2_y);
활동 2. 공의 충돌 구현하기 (운동량 보존과 운동에너지 보존을 활용)
활동 2의 코드를 실행해 본 결과가 어떤가요? 충돌 효과가 나타나기는 하는데 몇가지 이상한 부분이 있습니다.
첫번째로 공의 갯수를 늘려보겠습니다. 공의 갯수가 늘어나면 공이 생성될 때 충돌하면서 생겨나는 공들이 생깁니다. 공의 영역이 겹친채로 되는데 공의 충돌 위치를 보정해주어야 하는 부분이 필요합니다.
두번째로 충돌 과정을 계속 보고 있으면 약간 이상하게 충돌하는 경우를 볼 수 있습니다. 어떤 부분일까요? 바로 스쳐지나가듯이 비껴 맞을 때 입니다.
현실에서는 비껴 맞은 두 공의 운동과 활동 2 실행결과와는 약간 다르게 보입니다. 활동 2의 결과에서는 비껴 맞았음에도 불구하고 반대 방향으로 튕겨지는 것을 볼 수 있습니다. 왜 그럴까요?
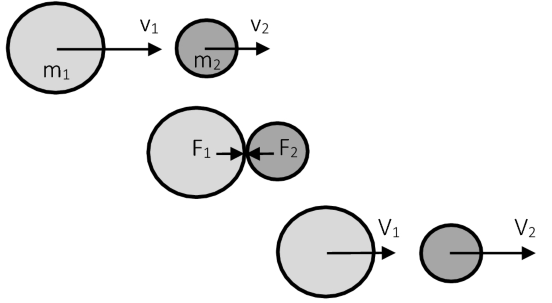
그 이유는 바로 공의 크기가 있어서 공이 충돌할 때 공의 운동 방향이 충돌시 주고받는 힘의 방향과 일치 하지 않습니다. 아래 그림처럼 대부분의 충돌은 충돌시 주고 받는 힘의 방향(두 공의 중심을 잇는 방향)과 충돌 속도($u_1$, $u_2$)의 방향이 어긋나게 됩니다.
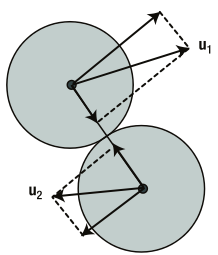
활동 2에서는 공의 크기와 상관없이 충돌이 일어나면 공의 운동 방향과 두 공의 중심을 잇는 선이 일치한다고 가정하고 구현된 것입니다. 이런 경우는 입자의 크기가 아주 작을때만 적용할 수 있는 것입니다.
그러면 크기가 있는 공이 충돌할 때 어떻게 해야 할까요? 위의 충돌 그림에 바로 답이 있습니다. 그림을 유심히 살펴보면서 아래 과정을 읽어보세요.
충돌을 감지한다.
충돌 바로 직전 위치로 재조정한다.
충돌 전 속도를 두 공의 중심을 잇는 방향 성분(normal)과 두 공의 충돌면에 평행한 (tangential) 방향 성분으로 분해한다. (이때 벡터의 내적을 활용)
공의 중심을 잇는 방향 속도 성분(normal)끼리만 충돌 공식을 적용하여 충돌 후 속도를 구한다.
충돌 후 구한 속도와 처음에 구한 충돌면에 평행한 방향 성분(tangential)의 속도를 벡터합한다.
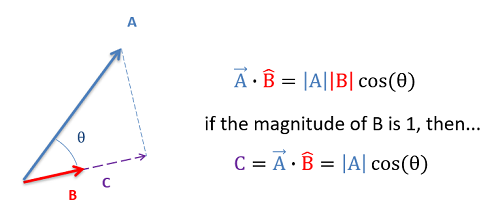
추가적으로 3번 과정에서 벡터의 내적을 이용하여 벡터를 임의의 방향으로 분해하는 방법은 다음과 같습니다.
벡터 내적 공식 : $\vec{A} \cdot \vec{B} = \left\vert A \right\vert \left\vert B \right\vert cos(\theta) = (A_xB_x) + (A_yB_y) $
벡터 A와 길이가 1인 벡터 B를 내적하면 A벡터를 B방향으로 분해한 벡터와 크기가 같다.
위의 과정을 활동 3을 통해 구현해 보도록 합시다.
활동 3. 공의 충돌 개선하여 구현하기 (크기를 고려)
활동 3의 실행해보면 활동 2보다 더 정확한 충돌이 일어나는 것을 확인할 수 있습니다. 우리는 운동량 보존과 운동에너지 개념을 이용하여 가상세계에서 물체의 충돌을 성공적으로 구현할 수 있었습니다.
오늘의 과제
그럼 지금까지 배운 중력과 충돌을 동시에 적용해 보도록 하겠습니다. 우리가 구현한 물리 엔진이 얼마나 잘 작동하는지 확인해 봅시다. 아래 코드를 draw() 함수 안에 중력을 설정하고 각 공에 적용해서 실행해 봅시다.
function draw(){
let gravity = createVector(0, 0.2);
...
...
balls[i].applyForce(gravity);
}