탄성력

1. 탄성력의 구현

금속 용수철이나 고무봉 등은 외부에서 힘이 가해지지 않았을 때 고유의 모양, 1차원적으로만 한정해 보면 자연적인 길이를 갖습니다. 이런 자연스러운 길이는 외부에서 힘이 가해지면 늘어나거나 줄어들게 되는데, 이때 원래 모양으로 돌아오려는 복원력이 작용하게 되며 이런 성질을 탄성이라고 합니다.

많은 탄성체에서는 변형의 정도가 작을 때 복원력과 변형량 사이에 비례관계가 성립(F = -kx) 하는데 이것을 그 발견자인 17 세기 영국 물리학자 로버트 훅의 이름을 기념하여 훅 법칙이라고 부릅니다.

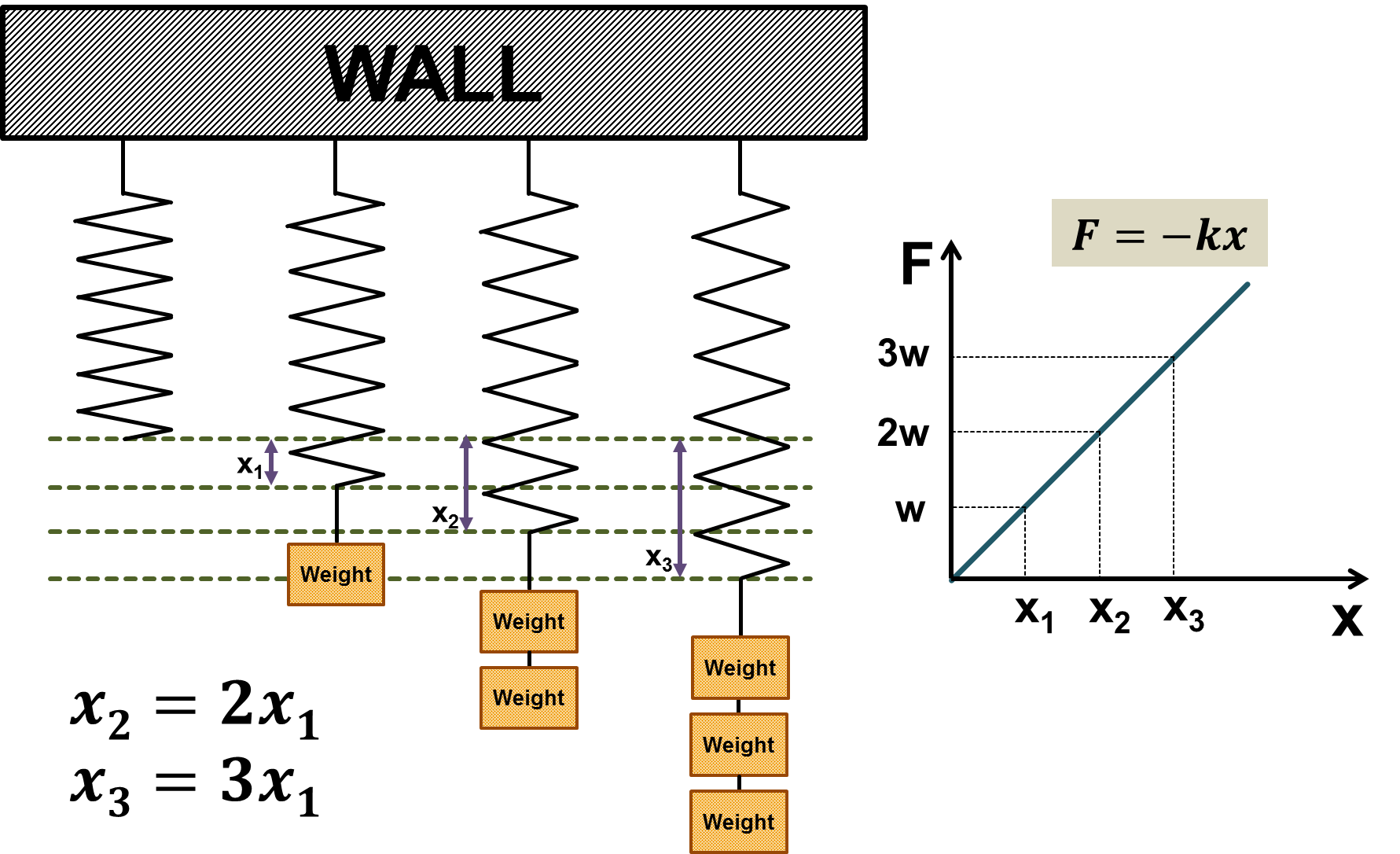
활동 1. 간단한 스프링의 구현

탄성력만 작용하는 상황에서 수평으로 움직이는 물체의 운동을 구현해 봅시다. 이 때 탄성력을 벡터로 계산하기 위해서 스프링이 연결된 고정점과 물체의 위치를 벡터로 정의합니다. 용수철의 기본 길이(restLength)에서 변형된 길이 dx에 해당하는 탄성력이 작용하고, 탄성력의 방향은 변형 방향의 반대로 작용합니다.

이를 코드를 표현하면 다음과 같습니다. 벡터의 방향과 크기를 변형할 때는 방향은 크기가 1인 벡터를 만들어 주는 normalize() 함수와 크기만큼 곱해주는 mult() 또는 setMag() 함수를 이용합니다.

  // 탄성력 계산
  let force = p5.Vector.sub(pos, anchor);
  let dx = force.mag() - restLength;
  force.normalize();
  force.mult(-1 * k * dx);  // force.setMag(-1 * k * dx)도 가능

활동 2. 용수철 진자 구현하기

앞에서 구현한 코드는 벡터로 구현하였기 때문에 2차원 진자 운동에서도 바로 적용이 가능합니다.

이제 중력과 탄성력이 동시에 작용하는 상황에서 용수철 진자를 구현해 봅시다. 추가적으로 물체를 마우스를 상호작용하는 방법도 함께 알아봅시다.

// 오일러 방법 적용하여 가속도-속도-위치 계산
acc = force.div(m);
acc.add(gravity);

vel.add(acc);
pos.add(vel);

// 마우스 상호작용
if (mouseIsPressed) {
pos.x = mouseX;
pos.y = mouseY;
vel.set(0, 0);
}

// 용수철 에너지 손실
vel.mult(0.99);

2. 탄성력과 입자계

원자와 원자 또는 분자와 분자 사이에는 전기력이 작용하여 물질의 형태를 유지하게 됩니다. 이는 마치 아래 그림과 같이 전기력이 용수철과 같은 역할을 한다고 볼 수 있는 것입니다.

이러한 성질을 이용하면 많은 입자로 구성된 물질의 운동도 탄성력으로 시뮬레이션 할 수 있답니다.

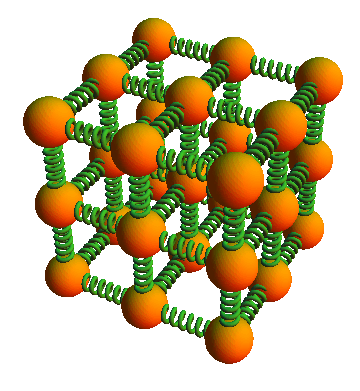
활동 3. 용수철 원자 모형 만들기

물체의 입자를 나타낼 Particle 클래스와 용수철의 기능을 수행할 Spring 클래스를 구현해 용수철 원자 모형을 구현해 봅시다.

여기서 클래스를 만드는 이유는 많은 입자들에서도 적용하기 위함입니다.

활동 4. 유연한 입자계 물질 구현하기

앞의 활동을 확장해서 여러개의 입자를 연결한 용수철 입자계를 만들어 봅시다.

용수철 입자계는 머리카락, 천 같은 유연한 물체를 시뮬레이션 할 때 적용할 수 있습니다.