벡터와 운동
1. 벡터와 속도
벡터(Vector)는 크기와 방향을 가지는 물리량을 나타내는 것으로, 위치, 속도, 가속도 같은 힘과 운동을 표현할 때 매우 유용합니다. 또한 운동하는 물체가 많아질수록 또한, 2차원, 3차원으로 차원이 높아질수록 벡터는 더 큰 힘을 발휘합니다.
p5.js 에서는 벡터 기능을 제공하며, 벡터의 기본 위치의 기준은 화면의 왼쪽 상단을 (0,0)으로 잡습니다. 그리고 화면 오른쪽으로 가면 x좌표값이 증가하고, 화면 아래쪽으로 내려가면 y좌표값이 증가하게 됩니다.
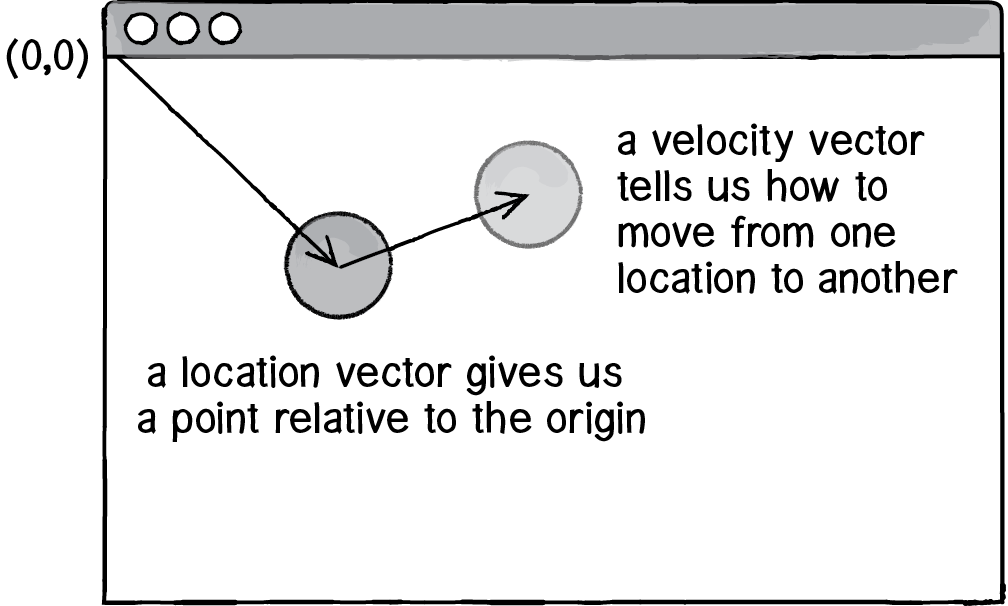
벡터를 사용할 때는 createVector()라는 함수를 사용하게 되며, 자세한 사용법은 p5.js 레퍼런스에서 자세히 확인할 수 있습니다.
그럼 물체의 운동을 표현할 때 벡터를 사용하지 않는 경우와 벡터를 사용한 경우를 직접 비교해보면서 벡터의 유용성을 살펴보겠습니다.
활동 1. 공의 등속 운동 (벡터를 사용하지 않은 경우)
활동 2. 공의 등속 운동 (벡터를 사용한 경우)
여러분 어떤가요? 코드가 약간 단순화 된 것이 보이나요? 그러나 이것은 벡터의 장점을 일부분만 보여준 것입니다. 앞으로 더 많은 입자, 3차원을 다루게 되면 벡터의 장점이 더욱 잘 나타날 것이니 기대하세요.
앞의 활동 2의 코드를 살펴보면 속도와 벡터를 이용하여 공을 움직에 만들어 보았습니다. 캔버스에서 움직임을 만드는 방법은 다음과 같습니다.
- 위치에 속도를 더한다.
- 위치에 객체를 그린다.
draw()함수는 무한히 반복되는 함수이기 때문에 객체의 위치는 계속 바뀌게 되는 것입니다.
활동 2의 코드에서 속도와 위치벡터를 바꿔보고 어떻게 움직임이 변하는지 살펴보세요.
2. 벡터와 가속도
이번에는 공의 움직임에 가속도를 추가해보겠습니다. 수업시간에 배운 가속도의 정의가 생각나나요?
가속도는 단위 시간동안의 속도 변화입니다. 속도도 이와 비슷한 개념으로 배운 것을 기억하실 것입니다.
속도는 단위 시간동안의 위치 변화이지요. 이렇게 시간에 따른 변화를 수학적으로는 미분, 적분의 개념으로 다룰 수 있다는 것도 배웠을 것입니다.

이렇게 연쇄적으로 가속도는 속도에 영향을 주고 속도는 위치에 영향을 줍니다. 가속도에서부터 변위를 구하는 과정을 코드로 나타내면 다음과 같습니다.
vel.add(acc); // 속도에 가속도만큼 벡터합을 해줍니다.
pos.add(vel); // 위치에 속도만큼 벡터합을 해줍니다.
물론 이 방법을 ‘오일러 방법’이라고도 하며 실제 운동과는 다르게 오차를 가집니다. 아래 그래프의 파란선이 실제 구하고자 하는 곡선이라면 빨간 선이 오일러 방법을 적용하여 구한 값을 나타낸 것입니다. 그래프를 비교해 보면 오차가 발생하는 것을 보실 수 있습니다. 물론 시간을 짧게 하면 오차를 줄일 수 있습니다.
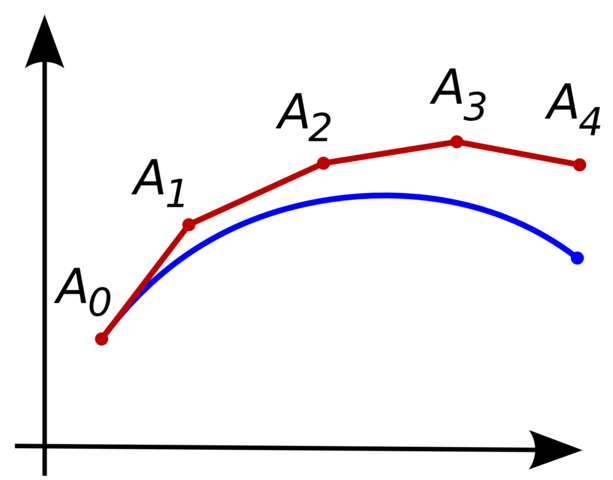
이러한 오차가 발생하는 이유는 우리가 수학 문제를 푸는 방법과 컴퓨터가 수학 문제를 푸는 방법이 다르기 때문입니다. 우리 인간은 모든 방정식을 풀 수 없고 특수한 경우만 그 값을 구할 수 있습니다. 그러한 풀이를 해석학적으로 답을 구한다 라고 합니다.
예를 들면 0 = x2 - 2 의 해를 구하면 $\sqrt{2}$, $-\sqrt{2}$ 를 구할 수 있습니다. 우리는 해를 구했다고 하지만 $\sqrt{2}$는 무리수이기 때문에 1.414… 라는 값을 정확하게 끝까지 알지 못합니다. 그렇지만 인간은 $\sqrt{2}$를 끝까지 숫자로는 표현은 못해도 가로, 세로 길이가 1인 직각삼감형의 빗면의 길이가 $\sqrt{2}$ 라고 하는 방법으로 이 값이 어떤 값인지 해석학적으로 표현할 수 있습니다.
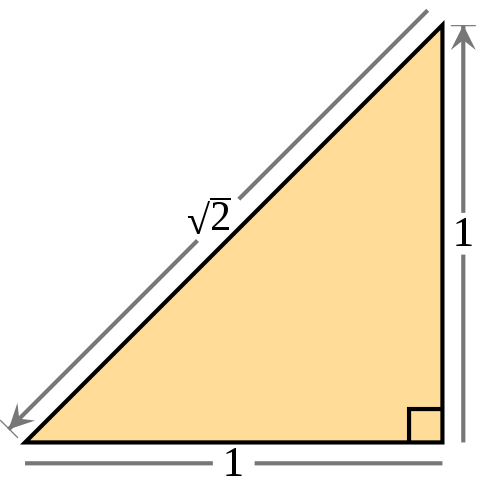
그러나 컴퓨터는 $\sqrt{2}$를 정확하게 표현할 수 없답니다. 그 이유는 컴퓨터의 메모리에도 한계가 있고 무한의 개념을 이해할 수 없기 때문에 0,1 숫자로밖에 표현하지 못합니다. 그래서 컴퓨터는 수학문제를 풀 때 숫자로 밖에 해석할 수 밖에 없고 이것을 수치해석이라고 합니다.
간단하게 말하면 기울기나 근사식, 수열의 점화식을 이용해 숫자를 계속 대입해 가면서 계산을 반복하여 근사값을 구하는 방법입니다. 이 방법이 무식하게 보일지 몰라도 컴퓨터는 인간보다 빠르고 지치지 않기 때문에 이런 방법이 힘을 발휘합니다. 너무 복잡해서 인간이 풀 수 없는 수학 방정식도 컴퓨터는 수치적으로 계속 계산을 하면서 답의 근사값을 찾을 수 있답니다.
이렇게 컴퓨터가 사용하는 대표적인 수치해석적인 방법이 바로 오일러 방법입니다. 오일러 방법은 오차가 다소 크게 나타나지만 단순하고 빠르게 계산할 수 있다는 장점이 있습니다. 우리가 알고 있는 미적분 개념을 아주 간소하게 적용했다고 보시면 됩니다.
물론 오일러 방법은 더 정확한 시뮬레이션을 만들때는 부적합합니다. 그래서 여러 수학자나 과학자들은 오일러 방법외에 더 정확한 수치해석 방법들을 많이 개발해 놓았습니다. 대표적으로 룽게-쿠타 방법 등이 있습니다. 그러나 이 방법들은 많은 컴퓨터 자원을 소모하기 때문에 계산 시간이 많이 걸립니다.
그래서 앞으로 우리가 만들 물리 엔진이나 시뮬레이션은 오차가 있지만 빠른 오일러 방법으로 구현하려고 합니다. 그럼 이제부터 힘이 작용하는 운동에서는 이 방법을 사용하도록 하겠습니다. 활동2의 공에 일정한 가속도를 가지도록 해보겠습니다.
활동 3. 공의 등가속운동
실제로 실행을 시켜보면 가속도에 의해서 속도가 점점 빨라지는 것을 볼 수 있습니다. 그런데 속도는 계속 커지기 때문에 오랫동안 실행하면 속도값이 무한히 커질 위험이 있습니다. 그래서 속도에 최대값을 두어 제한을 해보겠습니다.
vel.add(acc); // 속도에 가속도만큼 벡터합을 해줍니다.
vel.limit(10); // 속도의 최대치를 10으로 제한합니다.
pos.add(vel); // 위치에 속도만큼 벡터합을 해줍니다.
여러분이 직접 활동3의 코드를 수정해서 다시 실행해보십시요.
그럼 이번에는 운동에 다양한 변화를 주기 위해서 랜덤한 가속도를 주어볼까요? 가속도를 랜덤하게 만들기 위해서 p5.Vector.random2D() 함수를 사용해 보도록 하겠습니다.
acc = createVector(0, 0); // 가속도를 0으로 초기화
...
acc = p5.Vector.random2D(); // 임의의 방향으로 크기1의 벡터가 만들어짐
vel.add(acc); // 속도에 가속도만큼 벡터합을 해줍니다.
vel.limit(10); // 속도의 최대치를 10으로 제한합니다.
pos.add(vel); // 위치에 속도만큼 벡터합을 해줍니다.
활동 4. 공의 랜덤한 가속운동
랜덤한 가속도로 인해 보다 운동이 다양해졌다는 것을 알 수 있었죠?
오늘의 과제
처음 속도의 크기와 방향, 가속도의 크기와 방향을 조정해서 여러분만의 가속도 운동을 만들어 클래스룸 댓글에 공유를 해주세요.