군집 행동
1. 복잡계(complex system) 행동
지금까지 살펴본 자율 에이전트는 무언가를 찾아 움직이거나 배회하며, 흐름장 위에서 패턴을 가지며 이동할 수 있었습니다. 하지만 각각의 자율 에이전트는 독립적인 개체로 존재하며 다른 개체들과 상호작용하지는 못하였습니다.
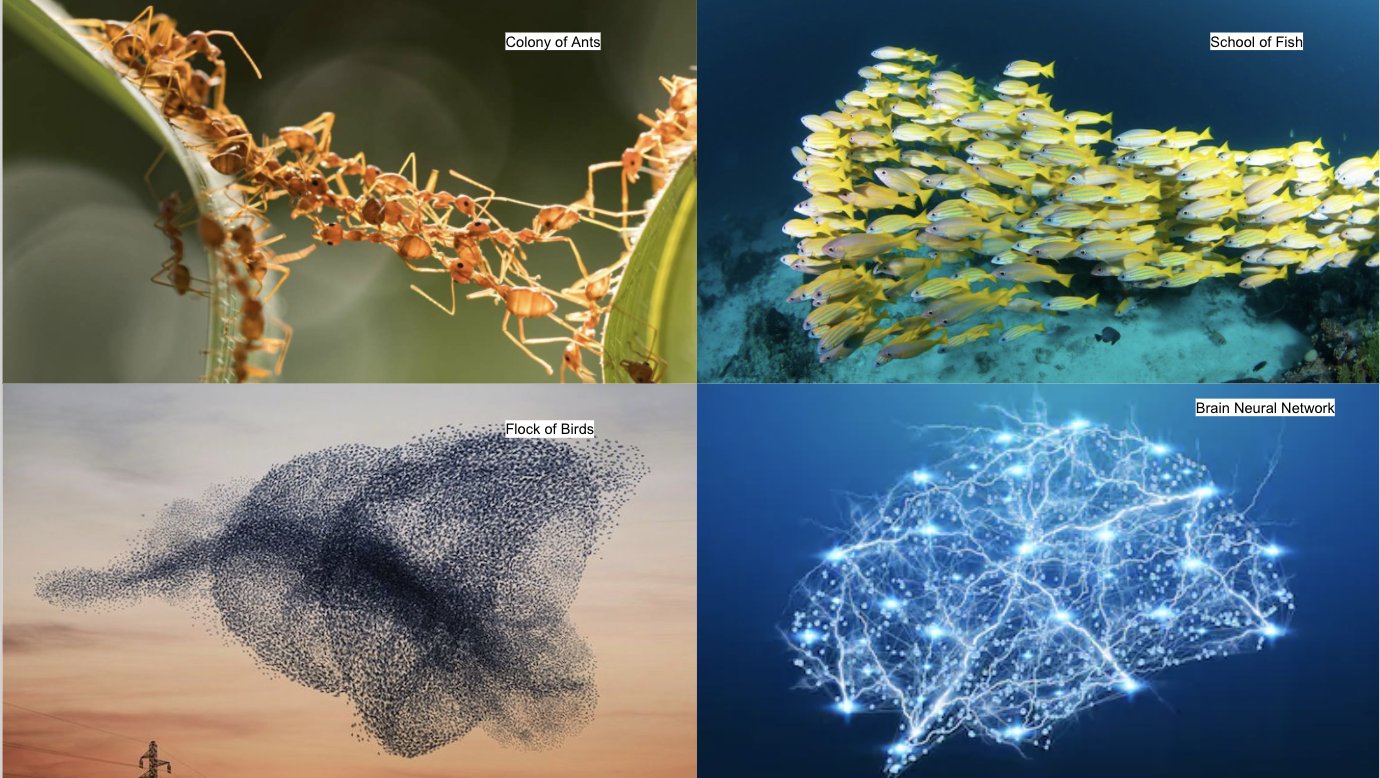
개미 1마리는 자율 에이전트입니다. 개미는 스스로 환경을 확인하고(감각을 사용해 방향 또는 화학적 신호를 감지) 이러한 신호를 기반으로 움직일지를 결정합니다. 하지만 단독으로 활동하는 개미가 둥지를 만들고, 먹이를 모으고, 여왕 개미를 지킬 수 있을까요?
개미는 자기 주변의 가까운 환경만 이해할 수 있지만 개미가 군집을 이루게 되면 다양한 목작을 달성할 수 있는 복잡계를 이루게 됩니다. 복잡계는 일반적으로 ‘다수의 대상이 합쳐져 단순한 기능 이상의 복합적인 기능을 발휘하는 시스템’으로 정의합니다. 복잡계를 구성하는 각각의 요소는 굉장히 단순하지만 이들이 모여 계(시스템)을 이루면 전체적인 행동이 굉장히 복잡해지게 됩니다.
2. 군집(flocking) 행동
군집은 새, 어류, 곤충 등에서 자주 볼 수 있는 특징으로, 동물들이 모여 만들어지는 가지는 집단으로 복잡계의 특성을 가집니다. 1986년 Craig Raynolds는 군집 행동 알고리즘을 만들어 아래와 같이 제안하였습니다.
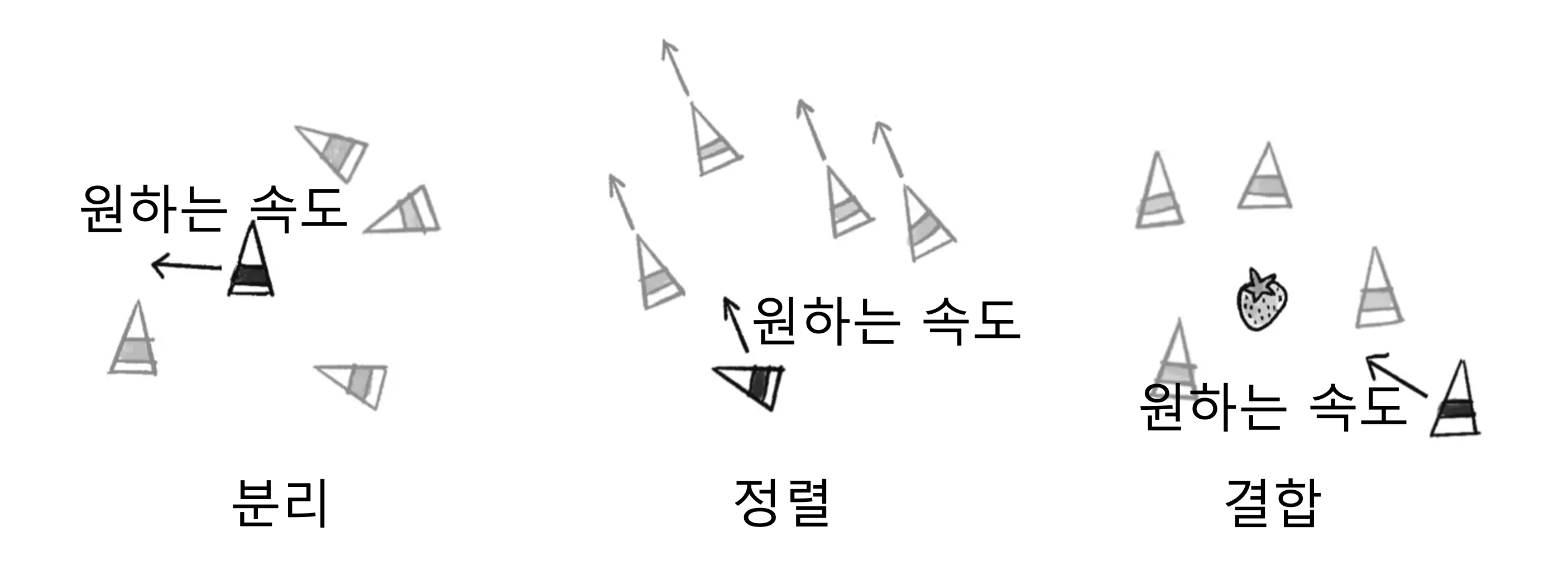
- 분리 (seperation): ‘회피’라고도 하며 이웃한 대상과 충돌을 피하려는 행동입니다.
- 정렬 (align): ‘복사’라고도 하며 이웃한 대상과 같은 방향으로 움직이려는 행동입니다.
- 결합 (cohesion): ‘집중’이라고도 하며 이웃한 대상들의 중심을 향해 움직이려는(집단을 유지하려는) 행동입니다.
각각의 행동은 다음과 같은 순서로 적용됩니다.
- 군집을 구현할 때는 조향력 공식(조향력 = 원하는 속도 - 현재 속도)을 사용합니다.
- 각각의 개체는 범위 안의 다른 개체들의 행동을 관찰합니다.
- 관찰한 결과를 통해 여러 개의 힘(분리, 정렬, 결합)을 합성하고 가중치를 부여합니다.
- 그 결과 간단한 규칙에 따라 움직이는 군집의 복잡한 집단 행동이 나타납니다.
이를 적용한 군집 행동 시뮬레이션을 위한 전체 코드의 구조는 다음과 같습니다.
const flock = [];
function setup() {
// 객체 생성
}
function draw() {
// 모든 객체들에 대한 관련 기능 실행
}
class Boid {
constructor(x, y) {
// 객체의 초기값 설정
}
update() {
// 오일러 방법으로 운동 계산
}
applyForce(force) {
// 합력 계산
}
flock(boids) {
// 각각의 개체에 대해 분리, 정렬, 결합 행동 실행
}
seperate(boids) {
// 분리 조향 행동
}
align(boids) {
// 정렬 조향 행동
}
cohere(boids) {
// 결합 조향 행동
}
show() {
// 자율 에이전트 그리기
}
edges() {
// 경계에서 움직임 설정
}
}
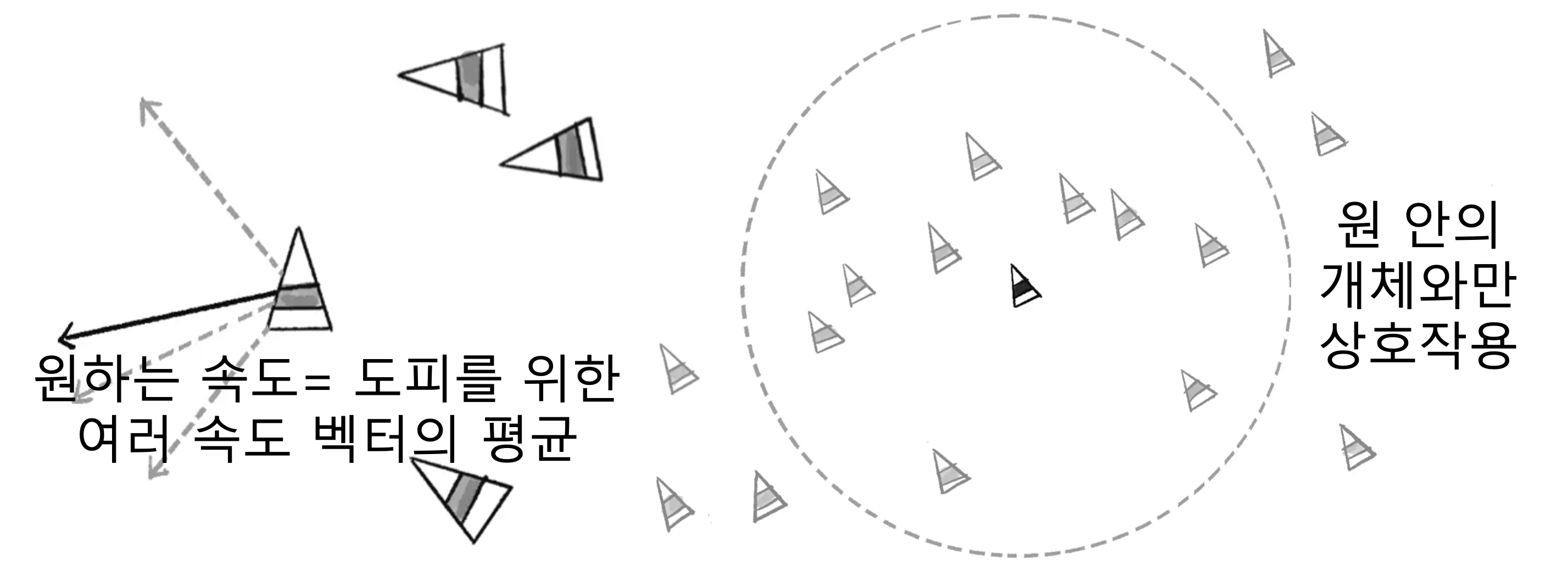
분리 (seperation)
‘분리’는 자율 에이전트들이 밀집하는 것을 피하기 위한 조향입니다. 거리가 너무 가까우면 적당히 멀어지게 조향하라는 것입니다. 기존 회피와 비슷하게 구현하면 됩니다. 단 회피를 위한 ‘원하는 속도’는 주변의 다른 개체들의 위치에 따라 거리 벡터를 평균하여 결정합니다.
seperate(boids) {
let desiredSeparation = 25;
let sum = createVector(0, 0);
let count = 0;
for (let i = 0; i < boids.length; i++) {
let d = p5.Vector.dist(this.position, boids[i].position);
if (d > 0 && d < desiredSeparation) {
let diff = p5.Vector.sub(this.position, boids[i].position);
diff.normalize();
diff.div(d); // 다른 개체가 멀면 조금 느리게 벗어나게 만들고 가까우면 빨리 벗어나게 벡터의 크기를 조절
sum.add(diff);
count++;
}
}
if (count > 0) {
sum.div(count);
}
if (sum.mag() > 0) {
sum.setMag(this.maxspeed);
let steer = p5.Vector.sub(sum,this.velocity);
steer.limit(this.maxforce);
return steer;
} else {
return sum;
}
}
정렬 (align)
‘정렬’은 주변의 자율 에이전트들과 같은 방향으로 조향하는 것을 말합니다. 특정 거리내의 있는 주변의 다른 개체들의 평균 속도를 계산하여 자신의 원하는 속도로 설정합니다.
align(boids) {
let neighborDistance = 50;
let sum = createVector(0, 0);
let count = 0;
for (let i = 0; i < boids.length; i++) {
let d = p5.Vector.dist(this.position, boids[i].position);
if (d > 0 && d < neighborDistance) {
sum.add(boids[i].velocity);
count++;
}
}
if (count > 0) {
sum.div(count);
sum.setMag(this.maxspeed);
let steer = p5.Vector.sub(sum, this.velocity);
steer.limit(this.maxforce);
return steer;
} else {
return createVector(0, 0);
}
}
결합 (cohesion)
‘결합’은 주변의 자율 에이전트들의 중심을 향해 조향하는 것을 말합니다. 특정 거리내의 있는 주변의 다른 개체들의 평균 위치를 계산하여 극 곳을 목표지점으로 설정합니다.
cohere(boids) {
let neighborDistance = 50;
let sum = createVector(0, 0); // Start with empty vector to accumulate all locations
let count = 0;
for (let i = 0; i < boids.length; i++) {
let d = p5.Vector.dist(this.position, boids[i].position);
if (d > 0 && d < neighborDistance) {
sum.add(boids[i].position); // Add location
count++;
}
}
if (count > 0) {
sum.div(count);
let desired = p5.Vector.sub(sum, this.position);
desired.setMag(this.maxspeed);
let steer = p5.Vector.sub(desired, this.velocity);
steer.limit(this.maxforce);
return steer;
} else {
return createVector(0, 0);
}
}
분리, 정렬, 결합 조향 행동을 모두 합하여 구현하면 다음과 같은 군집 시뮬레이션을 구현할 수 있습니다.
활동. 군집 행동을 하는 자율 에이전트
아래 p5.js 코드를 참고하면서 군집 행동하는 자율 에이전트를 구현해 봅시다.
const flock = [];
function setup() {
createCanvas(640, 400);
for (let i = 0; i < 300; i++) {
flock.push(new Boid(width / 2, height / 2));
}
}
function draw() {
background(220);
for (let boid of flock) {
boid.flock(flock);
boid.update();
boid.edges();
boid.show();
}
}
class Boid {
constructor(x, y) {
this.position = createVector(x, y);
this.velocity = createVector(random(-1, 1), random(-1, 1));
this.acceleration = createVector(0, 0);
this.r = 5.0;
this.maxspeed = 3;
this.maxforce = 0.05;
}
update() {
this.velocity.add(this.acceleration);
this.velocity.limit(this.maxspeed);
this.position.add(this.velocity);
this.acceleration.mult(0);
}
applyForce(force) {
this.acceleration.add(force);
}
flock(boids) {
let seperation = this.seperate(boids);
let alignment = this.align(boids);
let cohesion = this.cohere(boids);
seperation.mult(1.5);
alignment.mult(1.0);
cohesion.mult(1.0);
this.applyForce(seperation);
this.applyForce(alignment);
this.applyForce(cohesion);
}
seperate(boids) {
let desiredSeparation = 25;
let sum = createVector(0, 0);
let count = 0;
for (let i = 0; i < boids.length; i++) {
let d = p5.Vector.dist(this.position, boids[i].position);
if (d > 0 && d < desiredSeparation) {
let diff = p5.Vector.sub(this.position, boids[i].position);
diff.normalize();
diff.div(d);
sum.add(diff);
count++;
}
}
if (count > 0) {
sum.div(count);
}
if (sum.mag() > 0) {
sum.setMag(this.maxspeed);
let steer = p5.Vector.sub(sum,this.velocity);
steer.limit(this.maxforce);
return steer;
} else {
return sum;
}
}
align(boids) {
let neighborDistance = 50;
let sum = createVector(0, 0);
let count = 0;
for (let i = 0; i < boids.length; i++) {
let d = p5.Vector.dist(this.position, boids[i].position);
if (d > 0 && d < neighborDistance) {
sum.add(boids[i].velocity);
count++;
}
}
if (count > 0) {
sum.div(count);
sum.setMag(this.maxspeed);
let steer = p5.Vector.sub(sum, this.velocity);
steer.limit(this.maxforce);
return steer;
} else {
return createVector(0, 0);
}
}
cohere(boids) {
let neighborDistance = 50;
let sum = createVector(0, 0); // Start with empty vector to accumulate all locations
let count = 0;
for (let i = 0; i < boids.length; i++) {
let d = p5.Vector.dist(this.position, boids[i].position);
if (d > 0 && d < neighborDistance) {
sum.add(boids[i].position); // Add location
count++;
}
}
if (count > 0) {
sum.div(count);
let desired = p5.Vector.sub(sum, this.position);
desired.setMag(this.maxspeed);
let steer = p5.Vector.sub(desired, this.velocity);
steer.limit(this.maxforce);
return steer;
} else {
return createVector(0, 0);
}
}
show() {
let angle = this.velocity.heading();
fill(127);
stroke(0);
push();
translate(this.position.x, this.position.y);
rotate(angle);
beginShape();
vertex(this.r * 2, 0);
vertex(-this.r * 2, -this.r);
vertex(-this.r * 2, this.r);
endShape(CLOSE);
pop();
}
edges() {
if (this.position.x > width + this.r) {
this.position.x = -this.r;
} else if (this.position.x < -this.r) {
this.position.x = width + this.r;
}
if (this.position.y > height + this.r) {
this.position.y = -this.r;
} else if (this.position.y < -this.r) {
this.position.y = height + this.r;
}
}
}
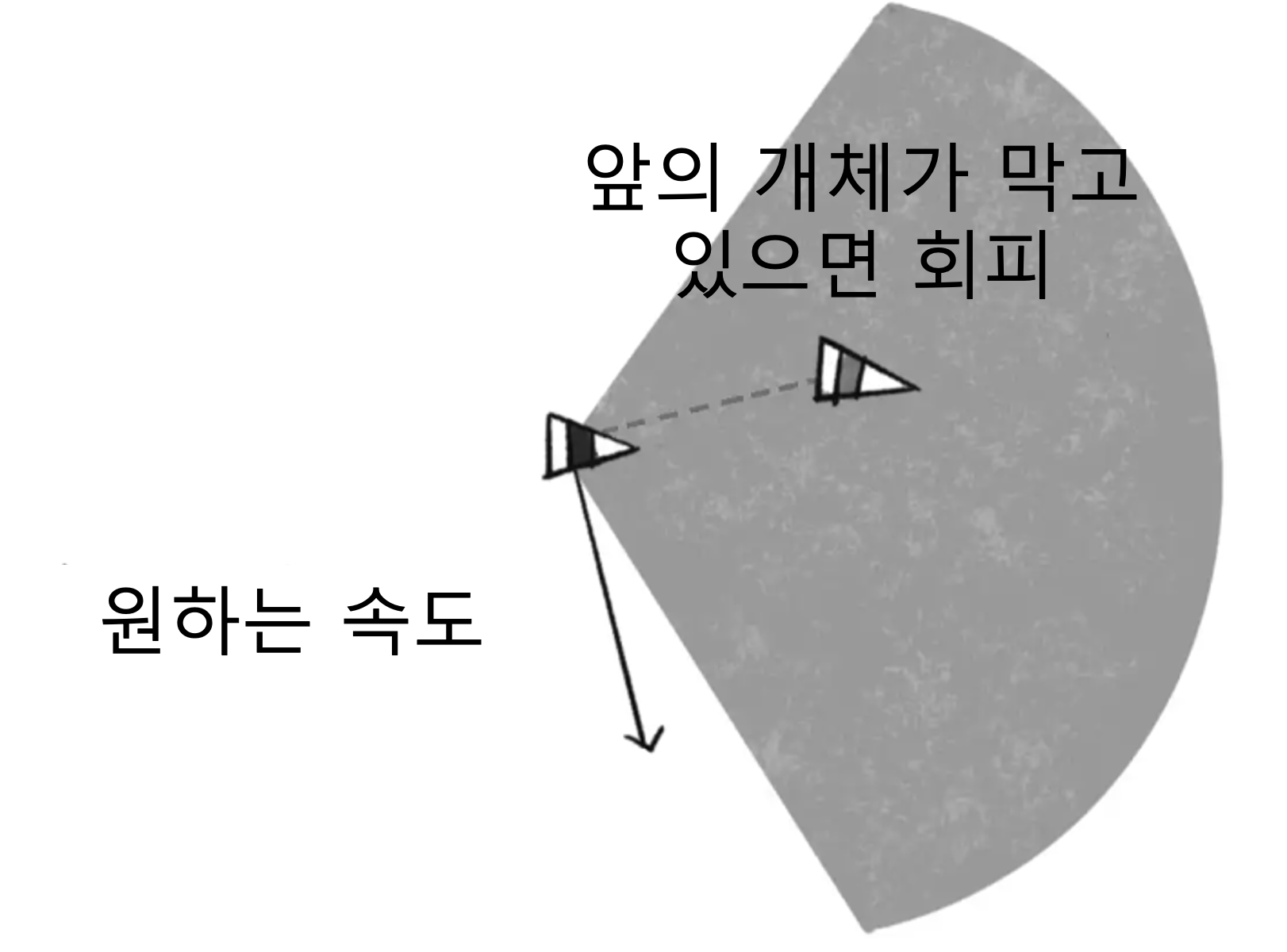
오늘의 과제
The Computiational Beauty of Nature(MIT Press, 2000)을 보면 세 가지 군집 헹동 알고리즘(분리, 정렬, 결합) 외에 네 번째 규칙을 제안하고 있습니다. 네 번째 규칙은 시야와 관련된 것인데 ‘앞에 시야를 가리는 개체가 있으면 회피하는 행동’입니다. 앞서 구현한 시뮬레이션에 네 번째 규칙을 적용해보세요.